Shortboard
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Funktionsterm von f
Zuerst die allgemeine Definition der Funktion \(f\).
Beachte: Der Mal-Punkt muss bei der Definition mitgeschrieben werden.

\(\\\)
Es gelten folgende Bedingungen:
\( \quad \begin{array}{ r c l c l } \text{größte Breite} & : & H( 1|0{,}25 ) & \Rightarrow & \; f(1)=0{,}25 \\[6pt] & & & \Rightarrow & f'(1)=0 \\[6pt] \text{Heckbreite} & : & P( 2| 0{,}1 ) & \Rightarrow & \; f(2)=0{,}1 \\[6pt] \text{Bugspitze} & : & S( 0| 0 ) & \Rightarrow & \; f(0)=0 \\ \end{array} \)
\(\\\)
Um \(f\) zu bestimmen, benötigen wir noch die 1. Ableitung von \(f\). Das Ableitungswerkzeug finden wir unter den mathematischen Vorlagen, die sich auf dem CAS neben dem aufgeschlagenen Buch befinden.

\(\\\)
Die 1. Ableitung von \(f(x)\)) definieren wir mit

\(\\\)
Zum Lösen des Gleichungssystems verwenden wir den \(solve\)-Befehl sowie ein Werkzeug, das wir ebenfalls unter den Vorlagen finden.


\(\\\)
Die gesuchte Funktion lautet
\( \quad f(x)=0{,}05 \cdot x^3 - 0{,}35 \cdot x^2 + 0{,}55 \cdot x \)
\(\\[2em]\)
Aufgabe 2 – Bugbreite und Heckbreite
Wir definieren Funktion \(f\) neu

\(\\\)
und berechnen die Werte.

\(\\\)
Die Breite beträgt am Bug \(27{,}308 \, cm\) und am Heck \(34{,}0278 \; cm\).
\(\\[2em]\)
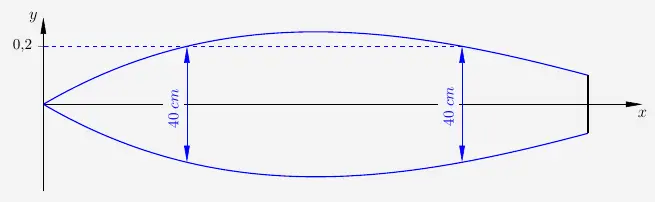
Aufgabe 3 – Breite von 40 cm
\(\\\)
Für die Breite gilt
\( \quad f(x) \; = \; 0{,}2 \)
Um die obige Gleichung zu lösen, verwenden wir den \(solve\)-Befehl. Dieser kann auf dreierlei Arten ausgeführt werden. Entweder schreiben wir wie oben den Befehl per Hand, benutzen die Menüführung

oder nehmen einfach die Tastenkombination \(\boxed{menu}\) \(\boxed{3}\) \(\boxed{1}\)
\(\\\)

\(\\\)
\(x=4{,}93543\) liegt außerhalb des Definitionsbereichs. Damit ist die Breite
\( \quad 1{,}5374 - 0{,}527166 \; \approx \; 1{,}01 \, m \)
\(\\[2em]\)
Aufgabe 4 – Öffnungswinkel an der Bugspitze
Der halbe Öffnungswinkel befindet sich zwischen der \(x\)-Achse und der oberhalb liegenden Tangente. Für den Winkel \(\alpha\) gilt also
\( \quad tan\left( \frac{\alpha}{2} \right) \; = \; m \)
\(\\\)
Dabei ist \(m\) die Steigung dieser Tangente, die mit
\( \quad m \; = \; f'(0) \)
\(\\\)
berechnet wird. Wir bilden zunächst die 1. Ableitung neu mit

\(\\\)
Für \(\alpha\) wählen wir die Variable \(a\) und berechnen diese mit

\(\\\)
Die Tangensfunktion ist natürlich eine periodische Funktion, so dass es unendlich viele Lösungen gibt. Mit einem geeigneten \(n1\), in diesem Fall scheint \(n1=0\) günstig zu sein, erhalten wir
\( \quad \alpha \; = \; 360 \cdot 0{,}16006 \; \approx \; 57{,}62^\circ \)
\(\\[2em]\)
Aufgabe 5 – Volumen des Surfbretts
\(\\\)
Das Volumen des Surfbretts wird berechnet mit
\( \quad V \; = \; Fl\ddot{a}che \; der \; Oberseite \times H\ddot{o}he \; des \; Surfbretts \)
\(\\\)
Dabei kann die Oberseite mit dem Integral berechnet werden.

\(\\\)
Das Volumen beträgt \(0{,}036667 \, m^3 \cdot 1000 \frac{l}{m^3} \; = \; 36{,}667 \, l\).
\(\\\)